Introduction
Heterogeneity in skeletal maturation is influenced by a complex interplay of factors, including genetic predispositions, the nutritional and growth status of the child, the onset of precocious puberty, hormonal variations, conditions related to pediatric endocrinology and metabolic disorders, and ailments affecting the musculoskeletal system [1-3]. The assessment of bone age, especially through methods that examine growth plates, is crucial not only for identifying precocious puberty and providing benchmarks for growth trajectories and future height predictions but also for managing conditions such as adolescent idiopathic scoliosis and determining the appropriate timing for orthopedic interventions in children with skeletal anomalies [3-6]. Thus, the appraisal of bone age using standardized methods is paramount for diagnosing, managing, and developing effective therapeutic strategies for these conditions.
Conventional methods for determining bone age in children, such as cervical vertebral maturation, the Roche-Wainer-Thissen criterion for knee assessment, and Risser’s sign for evaluating the iliac crest apophysis, are supplemented by more commonly used techniques like the Greulich and Pyle (GP) and Tanner Whitehouse (TW3) methods, which utilize radiographic images of the left hand. The GP method provides a straightforward way to estimate bone age by comparing the bony structures of the hand and wrist with a sex-specific collection of images that depict various stages of skeletal maturity. However, its accuracy can be compromised in cases of significant skeletal deformities, with the range of evaluative intervals in the image collection spanning from six months to a year. In contrast, the Tanner-Whitehouse (TW) approach assigns grades from A to I to each bone in the targeted area, comparing them to a standard dataset and aggregating these maturity scores to predict bone age. While the TW method is known for its complexity and precision, offering enhanced reliability, it also requires a more substantial time commitment [1,7].
The reliability of both GP and TW assessments depends on the subjective interpretation by radiologists, which can lead to variability in outcomes based on the evaluator's expertise [2,6]. This highlights the clinical need for more accurate and time-efficient methods for determining bone age. Recent advancements have led to the development of automated bone age assessment techniques that utilize AI technology, with commercial AI-based software solutions like BoneXpert and VUNO now available for clinical use. These innovations represent a significant shift towards more precise and dependable bone age assessment protocols.
Despite these technological advances, challenges remain, particularly in analyzing images affected by suboptimal quality or unusual skeletal structures. Furthermore, there is a significant lack of discussion concerning the effectiveness of post-processing techniques in conventional growth plate analyses.
Methods
This study is based on publicly available, anonymous X-ray image data; therefore, approval by the institutional review board and the requirement for informed consent were exempted.
In this study, we used training and validation data that had been preprocessed and normalized, utilizing Light hand X-ray images and comma-separated values (CSV) file-type labels for model training. We employed several models, including a convolutional neural network (CNN), Residual Network 50 (ResNet 50), Visual Geometry Group (VGG) 19, Inception V3, and Xception. To derive the predicted values for the test images, we stored the weight value corresponding to the smallest validation loss observed during the model training. The resulting values were saved in a comma-separated values file, and we evaluated each model by comparing the root mean square error (RMSE) values.
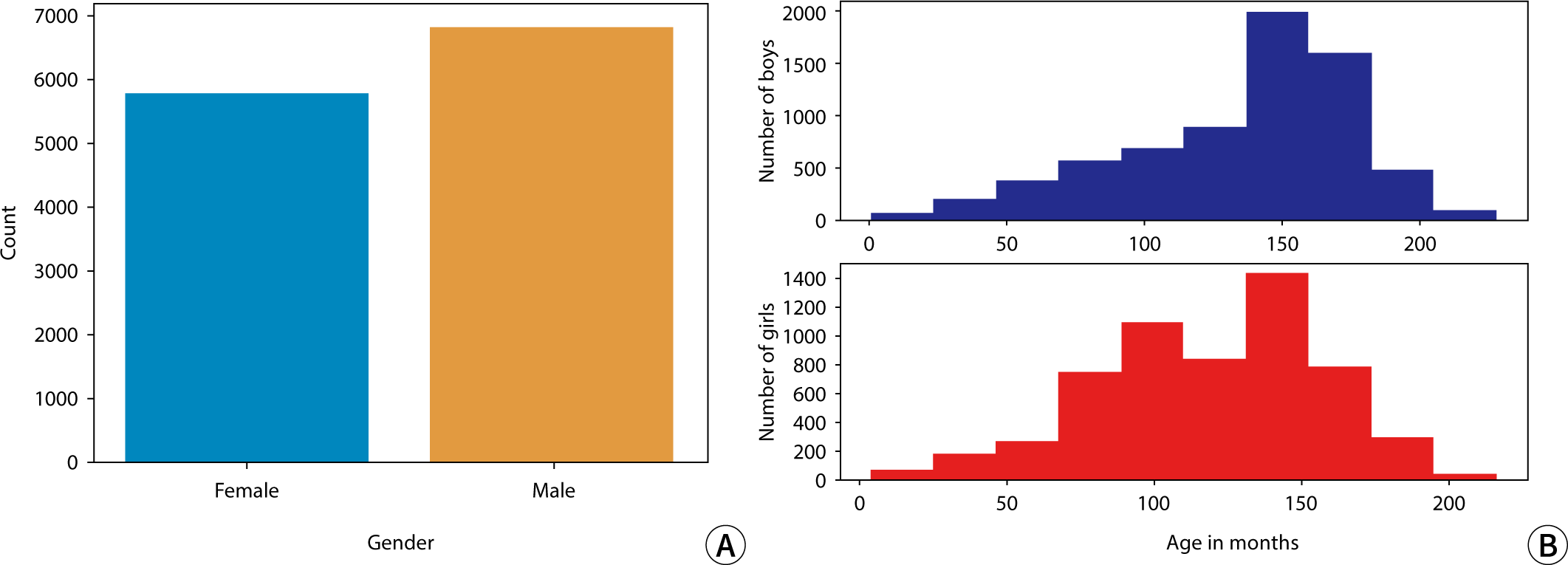
The data used in this study were obtained from the dataset released during the 2017 RSNA AI Pediatric Bone Age Challenge (Dataset 1), which was created by Stanford University and the University of Colorado and annotated by multiple expert observers. This dataset includes a total of 126,111 pediatric left-hand X-ray images, each labeled with the subject's sex and bone age. The age range of the subjects in these images spans from 1 month to 228 months and comprises 6,833 male and 5,778 female subjects. All data feature normalized resolution and have not been processed. Additionally, the data were collected in a multi-institutional setting, with labeling performed collaboratively by two pediatric radiologists from each institution. Table 1 shows specific details regarding the 2017 RSNA AI Pediatric Bone Age Challenge dataset. Data generated and/or analyzed during the current study are available in Dataset 2.
For the model training phase, 100,888 images, representing 80% of the total 126,111 images in the dataset, were used for training. The remaining 20%, or 25,123 images, were set aside for validation. The testing procedures utilized a subset of 100 images. Additionally, all images were resized to a resolution of 256×256 pixels in RGB format, and processing was carried out in batches of 32, using a random seed of 42 to ensure consistency. The training images underwent augmentation through vertical flipping, a technique used to increase data diversity and improve the model's generalization performance.
The Adam optimizer was used as the optimization function, and mean absolute error (MAE) served as the evaluation metric. The model underwent 50 epochs, each consisting of 300 steps, and it was subjected to both training and validation processes. These processes were essential for monitoring validation loss to determine the model's optimal performance, which was achieved when the loss value was at its minimum. The loss value and MAE from the validation phase confirmed the learning verification for each model on a monthly basis.
The formula for MAE is as follows:
n is the number of samples or data points, yi represents the actual or observed value, and yi' represents the predicted value.
The comparison of performance evaluations across models was shown as the distribution of differences between the labeled age and the predicted age.
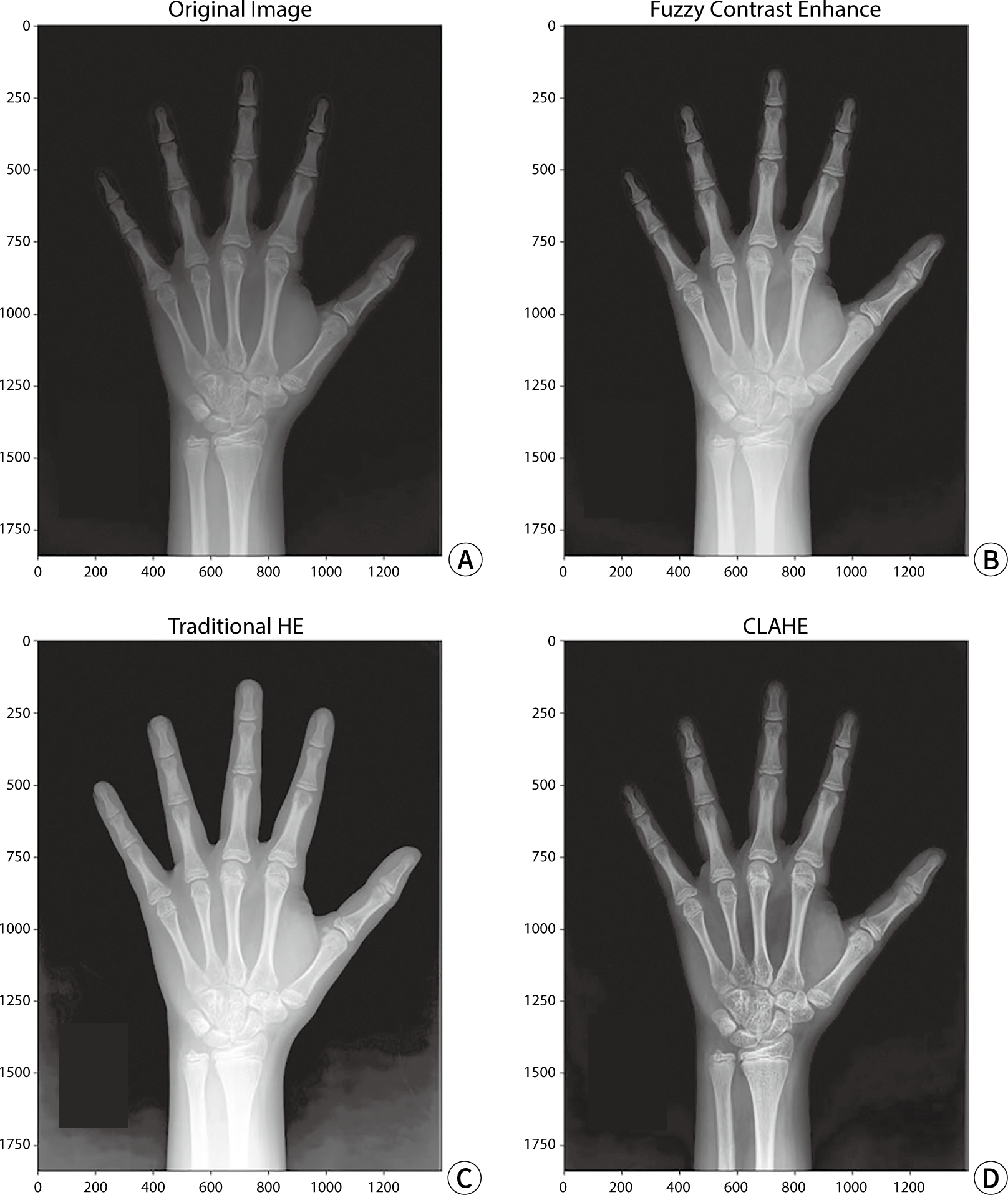
Contrast conversion procedures were conducted on 100 test datasets. Three distinct algorithms were employed for contrast adjustment: fuzzy contrast enhancement (FCE), histogram equalization (HE), and contrast limited adaptive histogram equalization (CLAHE). The FCE algorithm enhances image contrast by applying principles of fuzzy logic. This method involves fuzzifying the pixel intensities and then defuzzifying the resulting fuzzy set. The formal expression for the FCE algorithm is articulated as follows:
The conventional HE technique employs histogram equalization to enhance contrast. This algorithm involves calculating the histogram of the input image, followed by deriving the cumulative distribution function. Afterward, histogram normalization is performed, and the cumulative distribution function is used to adjust the pixel values in the image.
Conversely, the CLAHE algorithm utilizes a contrast-constrained adaptive HE approach to enhance image contrast. This method divides the image into discrete, small blocks, applying HE independently to each one. Contrast constraints are applied to improve the contrast within each image segment. Subsequently, all blocks are combined to produce the final image.
To assess the image quality of the contrast-transformed image, we analyzed several metrics, including the peak signal-to-noise ratio (PSNR), mean squared error (MSE), signal-to-noise ratio (SNR), coefficient of variation (COV), and contrast-to-noise ratio (CNR). The formulas for each metric are as follows.
Mp is the maximum possible pixel value, and MSE is the mean squared error between the original and distorted images.
A and B are the dimensions of the image. I(i,j) and K(i,j) are the pixel intensities of the original and distorted images, respectively.
SP represents the strength of the desired information in the image. NP represents the level of unwanted background noise in the image.
M represents the average contrast level in the image. SD denotes the variability or dispersion of noise within the image.
MC represents the average contrast level in the image.
A comprehensive assessment was conducted using 100 test sets to calculate the MAE and RMSE, thereby evaluating the accuracy of bone age estimation for each contrast-converted image. MAE was calculated according to Equation (1), and RMSE according to Equation (8).
n is the number of samples or data points, yi represents the actual or observed value, and yi' represents the predicted value.
Results
The sex distribution of subjects and the monthly age distribution for males and females in this study are presented in Fig. 1.
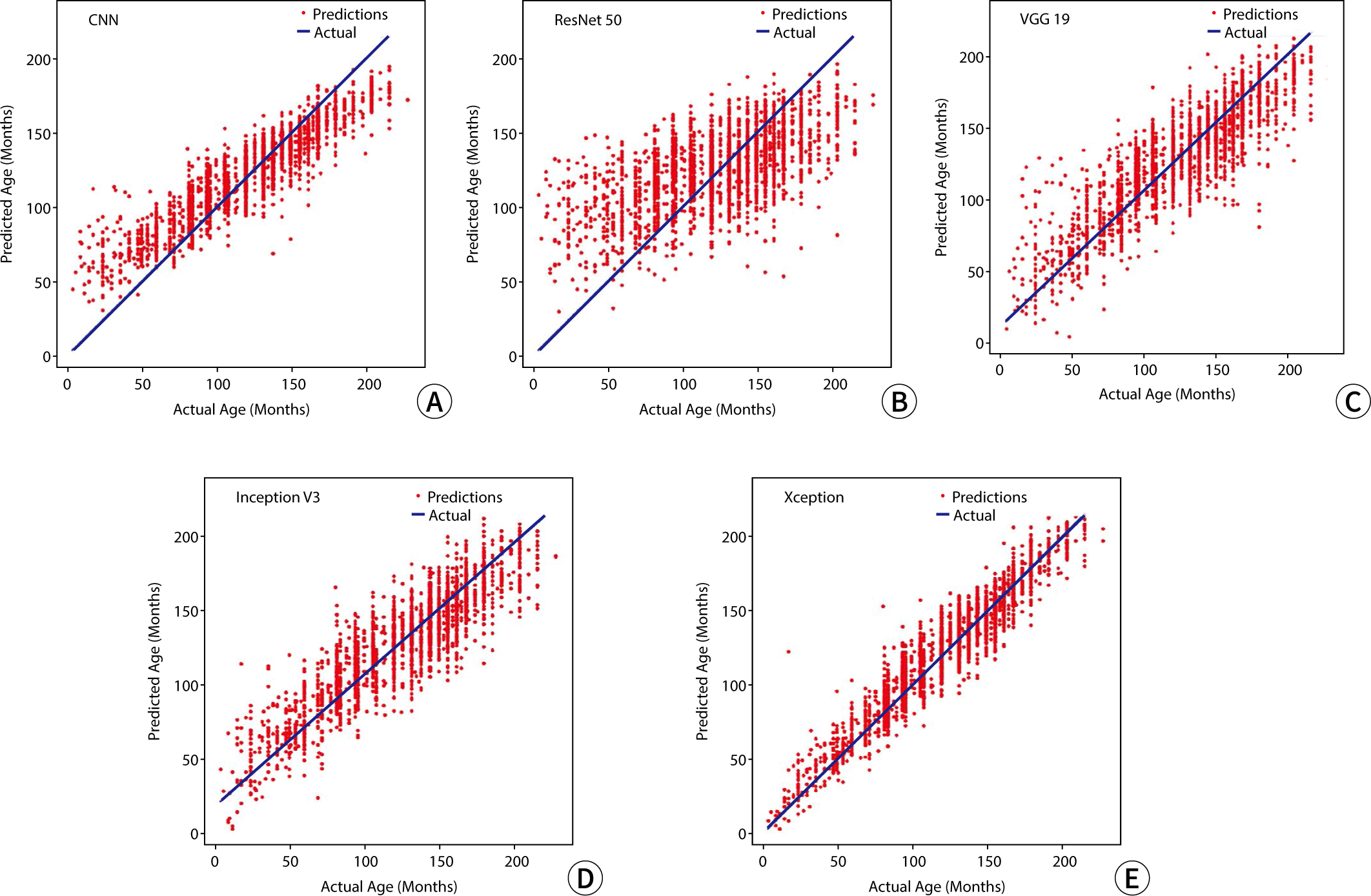
The RMSE values for the predicted bone age relative to the actual age, used as metrics to assess model performance in the study, were 50.91 for CNN, 55.29 for ResNet 50, 50.29 for VGG 19, 48.74 for Inception V3, and 41.12 for Xception. A graphical representation illustrating the outcomes of bone age prediction in relation to chronological age is shown in Fig. 2.
CLAHE, FCE, and HE were individually applied to the test data for model evaluation to perform contrast transformation. An example of a contrast-enhanced image is shown in Fig. 3.
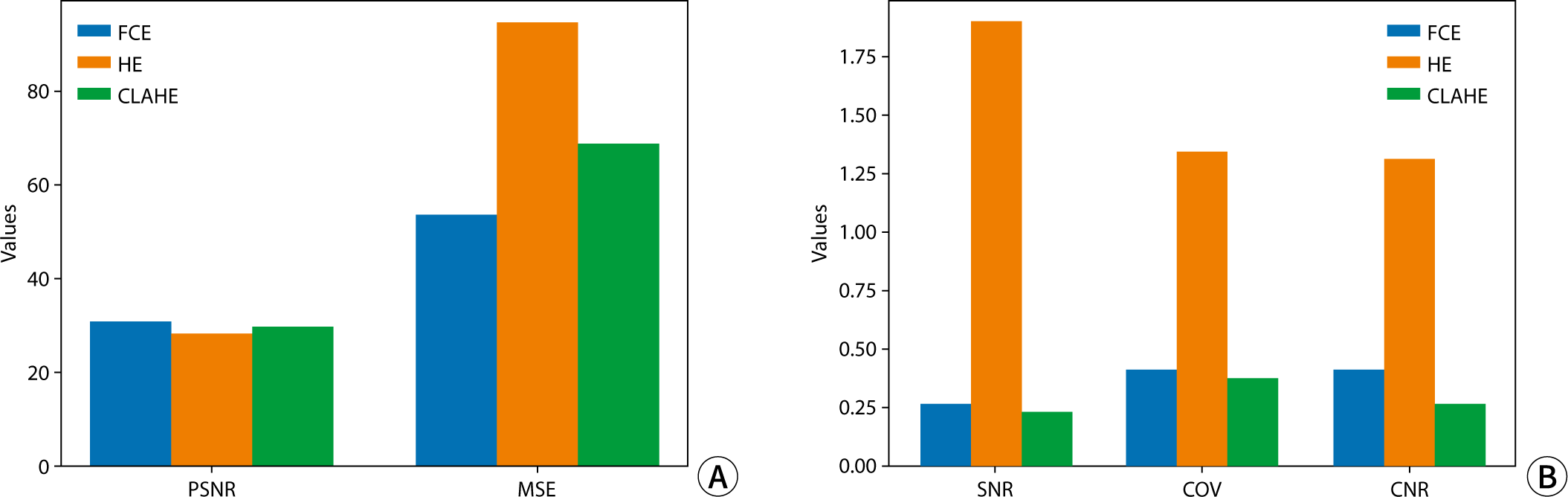
The quantitative assessment of each image utilized PSNR, MSE, SNR, and CNR (Fig. 4). In terms of PSNR and MSE values, image quality was ranked from highest to lowest as follows: FCE, CLAHE, and HE. Regarding factors evaluating noise and signal intensity in the images, SNR and COV exhibited higher values in the order of HE, FCE, and CLAHE. Specifically, for HE, SNR and COV were notably higher at 1.83 and 1.31, respectively, representing more than a sevenfold and threefold difference compared to other algorithms, respectively. In assessing contrast, CNR values were highest for HE, followed in descending order by FCE and CLAHE, with HE demonstrating the highest contrast at 1.29.
A total of 100 original and contrast-enhanced images were used as test data for bone age prediction in each model. Table 2 presents the MAE, RMSE, and P-value of the bone age prediction results across various models and contrast conversion algorithms. To facilitate comparison of bone age prediction performance using each contrast algorithm, evaluation results for the original images were also included. The accuracy of bone age prediction has improved, with statistically significant enhancements observed when using CLAHE in the CNN model, HE in the Inception V3 model, and HE in the VGG 19 model. In the Xception model, although the application of CLAHE and FCE algorithms led to better accuracy in bone age prediction, the improvements were not statistically significant.
Improvements in bone age prediction led to a reduction in MAE from 2.11 to 0.24 and a decrease in RMSE from 0.21 to 0.02.
Discussion
In this study, we implemented various bone age prediction models using identical parameters and evaluated the results by modifying the contrast of the test data. The Xception model demonstrated the most accurate bone age predictions. After adjusting the contrast, the PSNR and MSE metrics revealed that the FCE algorithm delivered the highest quality results. Furthermore, the quantitative assessments of SNR, COV, and CNR indicated that the HE algorithm produced the highest values. The prediction of bone age with contrast-adjusted images showed improved performance in 5 out of 15 cases compared to the original images. However, two of these five cases did not achieve statistical significance.
The primary cause of these outcomes was linked to the use of unprocessed images in the training dataset. The original images, obtained from various institutions, showed variations in how much of the left hand was captured, with some images featuring the left hand in non-horizontal positions. Although training the model with diverse datasets might enhance its applicability across different institutions, it could also negatively affect the model's performance. Future efforts will focus on acquiring preprocessed training data, which will involve adjusting the image contrast and ensuring that each image is horizontally aligned at the wrist bone through image registration. Additionally, in this study, the training and validation sets were separated in only one instance for individual model training. Future plans include the use of k-fold learning during model training to facilitate integrated learning and validation across the entire dataset.
Racial and ethnic disparities, along with variations in nutritional status and overall health, may affect bone age measurements. This suggests that applying bone age criteria directly to contemporary children and adolescents may not be appropriate [8]. Previous studies have developed deep learning-based bone age prediction models specifically optimized for Korean children and adolescents. These models use hand and wrist radiographs and have been evaluated for their validity compared to conventional methods [9].
This study demonstrated that the deep learning-based Korean model achieved superior bone age prediction accuracy compared to conventional methods, marking a significant advancement in precise growth assessment and clinical decision-making. The Korean bone age model reduces prediction biases and delivers more accurate age predictions across different age groups. Therefore, it is imperative to develop bone age prediction models that are customized for various racial groups.
Future research directions include preprocessing training data to ensure consistency in image quality and registration, implementing k-fold training to enhance model robustness, and fine-tuning models using datasets specific to Korean populations. These endeavors aim to enhance the overall accuracy and applicability of bone age prediction models in clinical practice, ultimately improving growth assessment and clinical decision-making for pediatric patients.
Conclusion
This study shows that when model learning is performed using non-preprocessed data, there is no significant difference in bone age prediction performance between contrast-converted images and original images. Rather than applying post-processing to the test dataset to improve predictions, it will be necessary to preprocess the training dataset.
